Formacja harmoniczna Nietoperz

Formacja Nietoperza została odkryta przez Scotta Carneya w 2001 roku przy współpracy z Jimem Kanem, któremu zawdzięczamy wprowadzenie zniesienia 88,6% do technik Fibonacciego. Jak łatwo się domyślić, zniesienie to jest kluczowym punktem formacji.

Budowa formacji Nietoperza

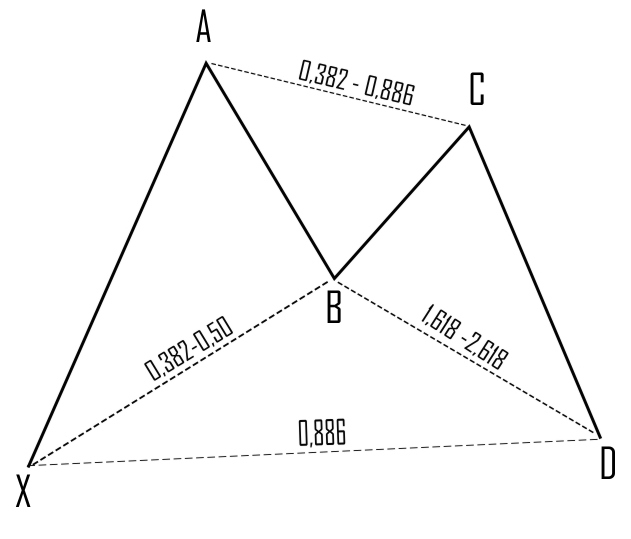
Wszystkie relacje jakie zachowane są w formacji Nietoperz, to:

|AD| = 0,886*|XA| – fala AD znosi 88,6% fali XA,
|AB|={0,382, 0,50}*|XA| – fala AB znosi 38,2% lub 50% fali XA (w bardziej liberalnym podejściu, wystarczy aby punkt B wypadł poniżej zniesienia 61,8%),
|BC|={0,382-0,886}*|AB| – punkt C powinien wypaść na jednym ze zniesień wewnętrznych Fibonacciego fali AB, z przedziału od 38,2 do 88,6%,
|CD|={1,618-2,618}*|BC| – punkt D powinien wypaść na jednym ze zniesień zewnętrznych Fibonacciego fali BC, z przedziału od 161,8 do 261,8%,
1,27*|AB|=|CD| – w idealnej formacji Nietoperza, występuje wydłużona formacja AB=CD. Liberalne podejście dopuszcza użycie innych współczynników Fibonacciego.

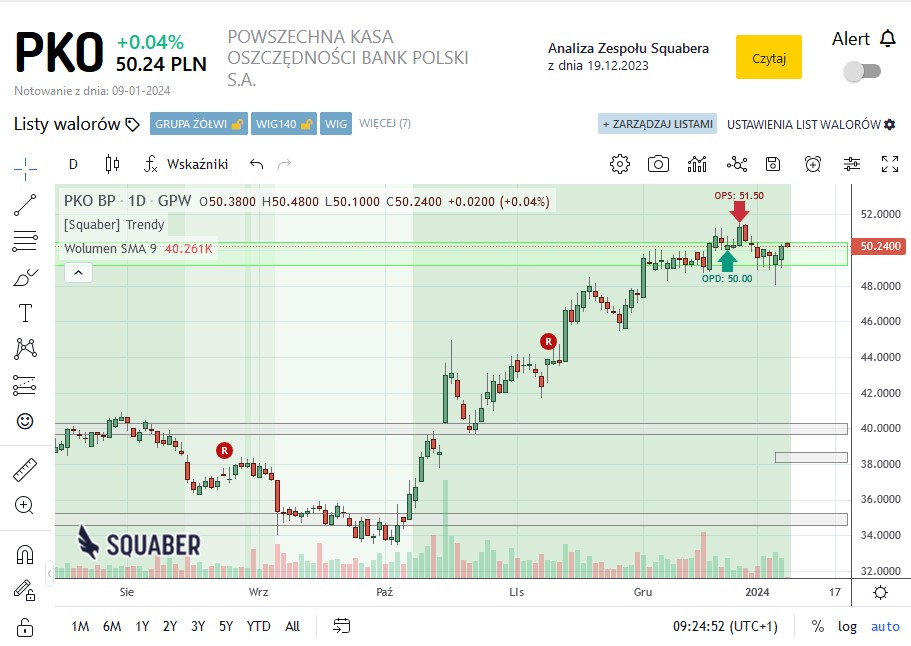
Wykorzystanie formacji harmonicznej Nietoperz – przykład 1

Formacja Nietoperz, tak jak większość formacji harmonicznych, może być zarówno formacją odwrócenia jak i kontynuacji trendu. Spójrzmy najpierw na przykład odwrócenia trendu, który prezentuje poniższy rysunek.

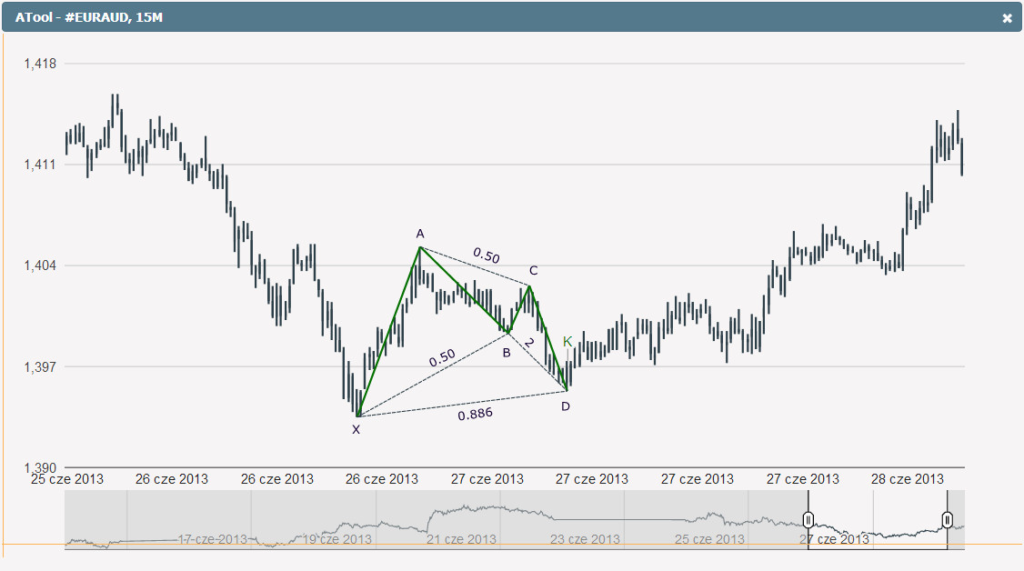
Przykład pochodzi z EUR/AUD (Euro vs Dolar Australijski) w skali piętnastominutowej. Po spadkach dużo większych niż może to objąć zrzut, uformowała się formacja harmoniczna Nietoperz, prognozując wzrosty. Jak łatwo zauważyć, na formację składa się pierwsza fala wzrostowa będąca odcinkiem XA oraz korekta prosta zawarta w odcinku AD. W wielu przypadkach pierwsza korekta nowego ruchu znosi większość impulsu właśnie do poziomu 88,6% i z tego powodu formację Nietoperza często można zaobserwować na szczytach bądź też dołkach. Spójrzmy na odwrotną sytuację.

Wykorzystanie formacji Nietoperza – przykład 2

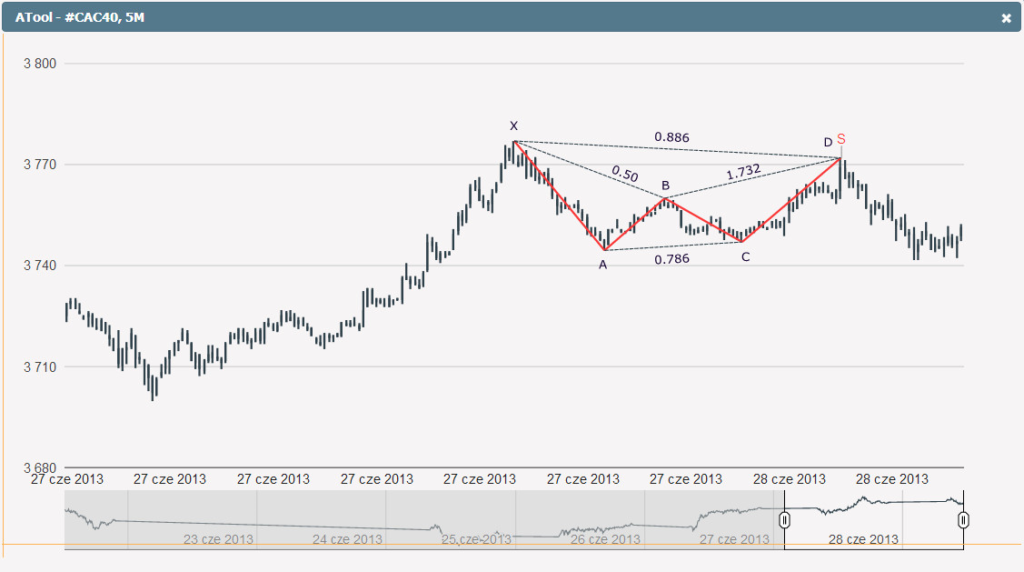
Formacje harmoniczne pojawiają się na wszystkich instrumentach oraz wszystkich interwałach czasowych. W tym wypadku przykład przedstawia CAC40 (główny francuski indeks giełdowy) w skali pięciominutowej. Odwrotnie do poprzedniego przykładu, tym razem formacja Nietoperza wystąpiła na szczycie, prognozując spadki które się zrealizowały. Jednak na rynku nie zawsze formacje wyglądają tak, jak na książkowych schematach i dlatego należy poszukiwać dodatkowych potwierdzeń przed zawarciem transakcji.

Formacja harmoniczna Nietoperz przykład odbiegający od schematu

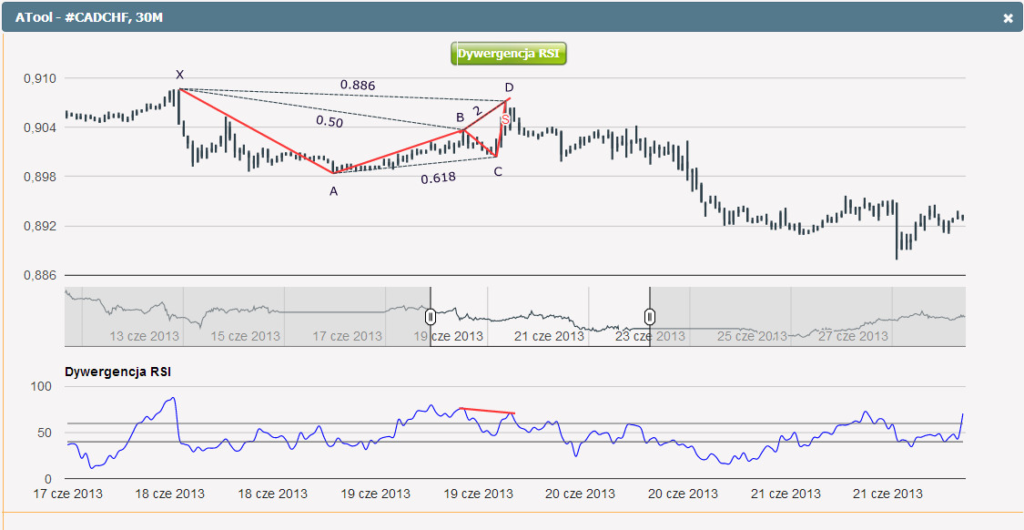
Ostatni rysunek przedstawia formację Nietoperza, która znacząco odbiega od schematu, jednak posiada zachowane wszystkie zależności. W takich przypadkach warto jednak poszukać dodatkowego potwierdzenia. W tym wypadku jest to dywergencja pomiędzy ceną  w punktach B oraz D a oscylatorem RSI. Dywergencja może również wystąpić pomiędzy punktami X oraz D. Innymi rodzajami potwierdzeń są formacje świecowe w punkcie D, poziomy wsparć i oporów czy linie trendu.

Mimo wykorzystanych potwierdzeń, należy pamiętać o tym iż to co czyni formację harmoniczną, jest precyzja. Punktem, który definiuje potencjalną formację jest punkt B. Jeżeli punkt B wypada na zniesieniu 61,8% ruchu XA to szukamy formacji Gartleya, jeżeli na zniesieniu 78,6% ruchu XA to szukamy formacji Motyla. W wypadku formacji Nietoperza punkt B musi wypaść na poziomie 0,382 lub 0,500. Jeżeli punkt B znajdzie się na innym poziomie, to nawet jeżeli cena odbije w punkcie D od poziomu 0,886, nie możemy mówić o formacji Nietoperza.

Następnym krokiem po zdefiniowaniu poziomu na jakim wypada punkt B, jest zaznaczenie odpowiedniego zniesienia punktu D, który zależy od danej formacji harmonicznej. Na równi z tym poziomem powinny wypaść inne zależności, specyficzne dla każdej formacji, tworząc klaster Fibonacciego aby było można ją uznać za harmoniczną. Oczywiście dokładność zależy od skali czasowej, gdyż wyznaczona strefa w skali M1 o 10 pipsowym rozstępie nie może być uznana za harmoniczną, jednak ten sam 10 pipsowy rozstęp na D1 będzie niewidoczny, a strefa będzie uznana za harmoniczną. Jest to kwestia uznaniowa i zależy od indywidualnego podejścia. Mimo tego, należy pamiętać, iż to nie kształt formacji czyni ją harmoniczną a precyzja występowania wszystkich zniesień na jednym poziomie.