Stopa zwrotu z portfela – prosta, TWR, a może MWR (IRR)?

Spis treści:

• Prosta stopa nie taka znowu prosta.
• Znaczenie przepływów w portfelu, zmian kapitału i wybranej stopy zwrotu.
• Efekty oddziaływujące na stopy MWR i TWR.
• Stopa MWR, czyli wewnętrzna stopa zwrotu IRR.
• Stopa TWR, czyli stopa ważona czasem.

Jedna wielkość, by wszystkimi rządzić

Podstawową miarą, którą jest zainteresowany każdy inwestor jest stopa zwrotu z prowadzonego portfela. Co bardziej zaawansowani dodają do tego jeszcze analizę poziomu ryzyka (mierzonego zmiennością uzyskiwanych stóp) oraz wskaźników, jak Sharpe, Treynor, czy alfa Jensena. Cała analiza nie może być jednak prowadzona w oderwaniu od realiów rynkowych, które wyrażają indeksy giełdowe, jak WIG20, często brane jako benchmarki – punkty odniesienia dla własnych wyników. Jeśli z portfela uzyskaliśmy stopę -5% to wynik ten wcale nie jest zły, jeśli szeroki rynek spadł chociażby o -15%…

Stopa zwrotu jest miarą relatywną, wyrażającą procentowo stopień przyrostu (albo spadku, w gorszym wypadku) wartości portfela względem zainwestowanego kapitału. Mamy zatem wzór:

obecna wartość portfela / zainwestowany kapitał – 1

Na tym sformułowaniu znajomość wyliczania tej miary przez większą część inwestorów się kończy. W istocie jest to tylko tzw. prosta stopa zwrotu – łatwa do zrozumienia i umożliwiająca proste porównania, ale kompletnie nieprzydatna, gdy tylko zmianie ulegnie zainwestowany kapitał.

TWR i MWR – pułapka na naiwnych?

Wśród profesjonalistów w grę wchodzą tylko stopy TWR i MWR, czyli odpowiednio ważone czasem i ważone pieniądzem. Fundusze inwestycyjne stosują tylko tą pierwszą, co część ich klientów uważa za mydlenie oczu, manipulowanie wynikami i zwykłą hucpę. Wynika to jednakże z niewiedzy, jak faktycznie stopy te działają i jakie mają zalety. Również w Squaberze zdecydowaliśmy się na stopę TWR i uznajemy ją za jedyną adekwatną miarę stopy zwrotu portfela. Co więcej, to właśnie TWR jest fundamentem standardów prezentacji wyników inwestycyjnych GIPS (autorstwa Insytutu CFA), które są globalnie przyjęte i stosowane przez instytucje finansowe – jest to złoty standard w branży. Interpretacja TWR i MWR jest jednakże czasem nieintuicyjna, dlatego w tym artykule postaramy się przystępnie wyjaśnić ten temat.

Jaskrawy przykład bezsensowności prostej stopy zwrotu

Wyobraźmy sobie następującą sytuację. Wpłacamy 1000 zł do portfela i w ciągu roku jego wartość wzrasta nam 1500 zł. Jaką stopę zwrotu osiągnęliśmy? W tym najprostszym przykładzie jest to naturalnie 50%. Teraz wyobraźmy sobie, że po 3 miesiącach od utworzenia portfela dopłaciliśmy do niego 5000 zł, które wypłaciliśmy jednak po kolejnych 7 miesiącach. Dzięki jednak zainwestowanym dodatkowym środkom – mimo, że na koniec okresu już ich w portfelu nie było (owych 5000 zł) – nasz czysty zysk urósł z 500 zł do 3000 zł. Teraz na koniec okresu, po roku, ponownie mierzymy naszą stopę zwrotu. Mamy zatem 3000 zł z kapitału początkowego 1000 zł = 200% ?! Wynik ten od razu wygląda na bezsensowny, a w oczy się rzuca użycie ponownie 1000 zł jako zainwestowanego kapitału.

Nie możemy użyć w podstawie wzoru początkowego kapitału portfela, bo uległ on zmianom na przestrzeni czasu, w którym mierzyliśmy stopę zwrotu. Tego właśnie punktu często nie rozumie duża część inwestorów, która chciałaby mierzyć tylko prostą stopę zwrotu i to ją uznaje za adekwatną. Jak widać jednak – wzór pozostaje wzorem, prosta stopa zwrotu nie uwzględnia zmian zainwestowanego kapitału w czasie, więc pokaże zafałszowane wyniki. No dobrze, ale ktoś mógłby powiedzieć – trzeba zmienić wpisywaną wielkość zainwestowanego kapitału w wzór. Tak… ale na jaką? Nie można po prostu wpisać zamiast 1000 zł, 6000 zł (1000+5000 wpłacone), bo 6000 zł nie było jako kapitał wpłacony w całym okresie pomiaru. Gdyby tak było, to prosta stopa zwrotu nie pozostawiałaby wątpliwości. Trzeba jakość to wyważyć i właśnie tym sposobem dochodzimy do innych miar stóp zwrotu, TWR i MWR, które niezaznajomione osoby tak chętnie krytykują jako oszukiwanie klientów.

Podsumowując ten fragment wywodu:

Prosta stopa zwrotu mierzy uzyskany zwrot wyłącznie względem początkowo zainwestowanego w portfel kapitału. Tym samym jakiekolwiek wpłaty i wypłaty kapitału w trakcie okresu pomiaru skutkują zafałszowaniem wyniku i czynią go bezsensownym. Prosta stopa zwrotu może być adekwatna jako uproszczona miara wyłącznie, jeżeli nic nie wpłacamy, ani nie wypłacamy z portfela.

Przepływy w portfelu

By zrozumieć istotę stóp TWR i MWR trzeba jeszcze pojąć dwa rodzaje przepływów gotówkowych, jakie mogą wystąpić w portfelu inwestora: zewnętrzne i wewnętrzne przepływy.

Zewnętrzne przepływy pieniężne to wszelkie wpłaty i wypłaty środków z portfela. Nie mają one żadnego wpływu na uzyskiwany zysk lub stratę, ale zmieniają poziom zainwestowanego kapitału. Zakłada się, że zarządzający portfelem (np. w funduszu inwestycyjnym, ale też inwestor, który to mierzy) nie ma wpływu na te przepływy (ich czas i wielkość), bo zależą one od decyzji klientów, co będzie bardzo ważne dalej.

Wewnętrzne przepływy pieniężne to przepływy w ramach portfela, np. decyzje o zakupie, sprzedaży walorów, wypłacone dywidendy, itp. Mają wpływ na wielkość zysku i straty, ale nie na zainwestowany kapitał. Uznaje się, że są one wynikiem decyzji zarządzającego portfelem.

Z perspektywy dużego funduszu z subportfelami podział ten może być bardziej zagmatwany, jednak na potrzeby inwestora indywidualnego jest wystarczający.

Pomiar zysku i straty

Jeśli w okresie pomiaru zaszły jakieś zmiany w poziomie kapitału, to licząc zysk/stratę musimy uwzględnić wszystkie zewnętrzne przepływy. Normalnie bierzemy wartość końcową i odejmujemy od niej wartość początkową. W tym wypadku natomiast (przyjmując, że zewnętrzne wpływy to wpłaty, a zewnętrzne wypływy – wypłaty) mamy:

Zysk/strata = Wartość końcowa – wartość początkowa – suma wpłat + suma wypłat

Warto wspomnieć, że możemy rozważać zysk netto i zysk brutto. Zysk netto to po prostu zysk brutto pomniejszony o wszystkie opłaty transakcyjne i podatki (np. Belkę) – taki też liczy nasz portfel w Squaberze.

Uśredniamy zainwestowany kapitał

Jak zobaczyliśmy, w prostym przypadku bierzemy tylko początkowo zainwestowany w portfel kapitał. Każda jego zmiana natomiast wymaga modyfikacji tej wielkości. Wzór to zatem:

Uśredniony kapitał = kapitał początkowy + suma ważonych wpłat – suma ważonych wypłat

Dlaczego ważonych? Bo liczymy je tylko za czas, kiedy środki te faktycznie pracowały. Jeśli do portfela dopłaciliśmy 5000 na pół roku, a stopę mierzymy roczną, to musimy dodać do kapitału początkowego 0,5 * 5000, bo wpłata ta pracowała przez pół okresu pomiaru (6 miesięcy z 12).

Proste i logarytmiczne stopy zwrotu

Liczenie stopy zwrotu w powszechnym rozumieniu to zwykły ułamek. Wynik ten zakłada pomiar liniowy odsetek od kwoty (zysku), ich wypłatę na koniec okresu pomiaru i brak procentu składanego (czyli odsetek od odsetek – zysk generuje dalszy zysk). Jest to zatem adekwatny pomiar w jednym okresie, np. w ciągu roku. Gdy już mierzymy stopę na przestrzeni kilku lat, to musimy te stopy przemnożyć, by uwzględnić efekty procentu składanego.

Wygodne są stopy logarytmiczne, gdzie zakłada się, że odsetki (zysk) są wypłacane niemalże ciągle i natychmiast reinwestowane po tej samej stopie zwrotu. Automatycznie zatem uwzględniają procent składany.

Stopy logarytmiczne mają tą interesującą właściwość, że stopy pojedynczych okresów wystarczy pododawać, żeby otrzymać wynik z wielu okresów. Jeśli zatem w jednym i drugim roku uzyskaliśmy stopy zwrotu 10%, to jeśli są to stopy proste, to trzeba je przemnożyć 1,1 * 1,1 = 1,21 = 21% zysku w dwa lata. Jeśli natomiast owe 10% to stopy logarytmiczne, to po prostu 10% + 10% = 20% i wynik ten będzie taki sam, gdybyśmy okresem pomiaru objęli od razu całe 2 lata (gdybyśmy to samo zrobili na stopa zwykłych, dodając wyniki za każdy rok, to wartości by się rozjechały, bo nie uwzględniłyby procentu składanego).

Co więcej, są one symetryczne i nie cierpią z powodu efektu bazy. Przy stopach zwykłych, by odrobić 50% straty, musimy wygenerować 100% zysku, by wyjść na zero, bo 100*0,5 = 50, a 50*2 = 100. Przy logarytmicznych 50% straty odrabia się poprzez 50% zysku, bo ln(50/100) + ln(100/50) = 0. Jakby tego było mało, jeśli mając stopę roczną, chcemy wyciągnąć stopę półroczną, to przy stopach zwykłych musimy wyciągnąć pierwiastek, a przy logarytmicznych wystarczy podzielić je na 2 – analogicznie przy wyborze innych okresów.

Właśnie dlatego stopy te są tak popularne w finansach, bo są po prostu wygodne do stosowania – nie trzeba martwić się przemnażaniem ich. Obie wersje można wygodnie przekształcać i przejść z jednej na drugą:

Stopa logarytmiczna = ln(1+stopa zwykła)

Stopa zwykła = e ^ (stopa logarytmiczna) – 1

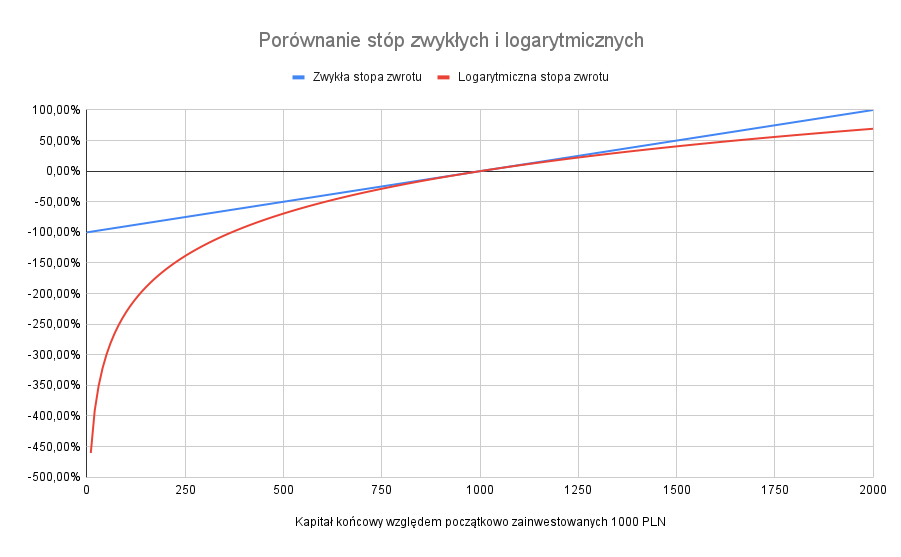
Stopy logarytmiczne mają jednak tą poważną wadę, że o ile są w miarę dokładne przy niewielkich wynikach (kilka procent), ich błąd względem stóp zwykłych lawinowo wzrasta, jak na poniższym wykresie, gdzie porównaliśmy wyniki. Z tego względu w Squaberze nie poszliśmy na skróty i w portfelach bazujemy na stopach zwykłych, które potem iloczynowo łączymy.

Stopa logarytmiczna zatem wykazuje większą procentowo stratę względem stopy zwykłej i mniejszy procentowo zysk (bo zakłada ciągłą reinwestycję odsetek, więc potrzeba relatywnie mniejszej stopy zwrotu, by wygenerować ten sam wynik końcowy). By utrudnić sobie jeszcze zadanie, można rozważać portfel prowadzony w wielu walutach, a więc chociażby składający się z akcji polskich i amerykańskich. Żeby adekwatnie wyliczyć w nim stopę zwrotu trzeba wybrać walutę bazową (złotówki czy dolary? Dla polskiego inwestora pewnie złotówki), a potem stosowne wielkości w walucie zagranicznej przeliczać przez adekwatny kurs walutowy. O ile możliwe jest to dla relatywnie niewielkiego portfela pod względem liczby walorów i transakcji, o tyle sprawa komplikuje się, gdy chcemy to zrobić dobrze na skalę masową. Z tego względu portfele składające się z walorów w wielu walutach są dopiero w Squaberze w planach.

Typy decyzji inwestora a stopy TWR oraz MWR

W trakcie swej działalności inwestor podejmuje generalnie 3 typy decyzji ważnych z perspektywy stóp zwrotu. Wyróżnia się tedy trzy działające na nie efekty:

• Efekt benchmarku – sama decyzja zarządzającego o inwestycji w wybrany benchmark, np. w WIG20.
• Efekt zarządzania – decyzja zarządzającego o zmianie składu portfela względem benchmarku – wag, wybranych walorów, itp. Inwestor indywidualny de facto nie myśli o efekcie inwestycji w benchmark, tylko często od razu zarządzania, tworząc własną kompozycję akcji.
• Efekt timingu – decyzje o zmianie wielkości zainwestowanego kapitału i czasu, gdy to następuje. Tutaj mamy do czynienia z zewnętrznymi przepływami pieniężnymi. Zakłada się, że zarządzający funduszem nie ma wpływu na efektu timingu, ale już inwestor indywidualny ma wpływ na wielkość inwestycji, więc wywołuje efekt timingu. Przykładowo może zdecydować, by wycofać kapitał na szczycie, a dołożyć go w dołku.

Efekty te są o tyle ważne, że stopa TWR obejmuje tylko dwa pierwsze, a MWR wszystkie!

Jeśli zatem zarządzający portfelem nie ma wpływu na wpłaty i wypłaty z niego, powinno się mierzyć zwrot z takiego portfela stopą TWR. Taki też jest rynkowy standard. Jeśli ma na nie wpływ, jak inwestor indywidualny, to formalnie powinna to być stopa MWR. Można zatem odnieść wrażenie, że w Squaberze powinna to być MWR. Tak jednak nie jest, zdecydowaliśmy się na TWR z kilku względów, które staną się jasne, gdy wyjaśnimy czym są te stopy.

MWR (Money-Weighted Return), czyli wewnętrzna stopa zwrotu (IRR)

MWR to po prostu IRR znana z Excela jako funkcja XIRR, inaczej wewnętrzna stopa zwrotu. MWR można wyliczyć na kilka sposobów, ale dopiero IRR jest prawdziwą MWR, dającą precyzyjny wynik, a nie jego przybliżenie. IRR to taka stopa zwrotu, która w zadanym okresie pozwala zdyskontować końcową wartość inwestycji i występujące zewnętrzne przepływy do początkowo zainwestowanego kapitału. Z drugiej strony jeśli użyjemy jej jako stopy zwrotu to pozwala urosnąć początkowemu kapitałowi i zewnętrznym przepływom do końcowej wartości inwestycji. Z tego względu, IRR trochę naiwnie zakłada, że zewnętrzne wpływy są finansowane taką samą stopą procentową jak IRR, a wypływy nią dalej reinwestowane. Jest to założenie nierealistyczne.

Co więcej, IRR jest wyliczana w sposób numeryczny (ręcznie powiedzmy, że byłoby to metodą prób i błędów) i może dawać wiele rozwiązań (wiele różnych IRR), a nawet w skrajnym przypadku żadnego! Wypłaty z portfela zwykle są oznaczane jako liczby dodatnie, zaś wpłaty (jako inwestycje) – ujemne. Ile zmian znaków – tyle IRR. Jeśli wpłaciliśmy i wypłaciliśmy na koniec, to mamy jedną zmianę znaku i pojedyncze (z reguły) IRR. Jeśli jednak wpłacaliśmy i wypłacaliśmy dalej, to za każdym razem, gdy zmienia się znak, tworzy nam się nowe IRR. Które jest adekwatne? Kalkulatory i arkusze kalkulacyjnie zwykle pokazują tylko pierwsze IRR, co wcale nie znaczy, że najlepsze…

Da się to obejść poprzez tzw. MIRR, czyli zmodyfikowaną wewnętrzną stopę zwrotu. Mówi się, że też jest to prawdziwa MWR, a nie jej przybliżenie. MIRR jest generalnie podobna to IRR, ale odrzuca nierealistyczne założenia o finansowaniu wpływów i reinwestycji wypływów po tej samej stopie, jak ona sama. Dzięki temu uzyskujemy tylko jeden, unikalny wynik. Jeśli zatem chcemy wyliczyć MWR, to generalnie proponowalibyśmy się skłonić ku ręcznemu wyliczeniu MIRR.

Szybkie przybliżenie MWR daje metoda Dietza, gdzie wszystkie zewnętrzne przepływy waży się wagą 0,5, tj. tak, jakby wystąpiły w połowie okresu pomiaru. Faktycznie zatem to proste uśrednienie zainwestowanego kapitału, o czym pisaliśmy na samym początku. Jeśli zmodyfikujemy metodę Dietza, ważąc przepływy względem czasu, przez który kapitał pracował, to otrzymamy kolejne lepsze przybliżenie IRR i niezłą, aczkolwiek nieprofesjonalną, miarę stopy zwrotu na własne potrzeby.

Zakłada się tu wszędzie, że przepływy zewnętrzne występują na koniec dnia, co jest raczej standardem. Jeśli mamy z nimi do czynienia na początek dnia, to musimy wzory stosownie zmodyfikować – tutaj większe problemy mają w działach rachunkowości funduszy inwestycyjnych, gdzie potrzeba precyzyjnych wyników dzień po dniu, a dość dodać, że mierzą się tam w końcu z wypłatami i wpłatami także w ciągu dnia, więc ważenie musiałoby być bardzo precyzyjne.

Podsumowując MWR:

• Uwzględnia wpływ efektu timingu, a zatem zależy od zewnętrznych przepływów pieniężnych, które mają wpływ na wielkość zainwestowanego kapitału. Jeśli zarządzający portfelem nie ma wpływu na te przepływy, to tej stopy używać zwyczajnie się nie da.
• Używa nierealistycznych założeń, wyjąwszy wersję MIRR. Czyste IRR jest również trudne do wyliczenia.
• Czyste IRR może dawać wiele rozwiązań, a w skrajnym przypadku nawet żadnego.
• MWR nie pozwala na porównania z innymi – jedynie z wybranym benchmarkiem, jeśli się je uzgodni.
• MWR jest zawsze stopą zwrotu za jeden okres – nie da się pojedynczych MWR połączyć w jedno za większy okres. W ten sposób można uzyskać tylko przybliżenie skumulowanej TWR, czyli kompletnie innej stopy!
• Nie da się zatem śledzić zmian stopy zwrotu portfela dzień po dniu. Próby ominięcia tego prowadzą do bezsensownych wyników – nie da się rozszerzać okresu pomiaru dzień po dniu i porównywać zmiany.
• MWR nie pozwala na pomiar ryzyka portfela (zmienności stóp zwrotu), więc nie policzymy z niej odchylenia standardowego. Skoro MWR jest za jeden okres – to nie ma rozrzutu wyników, bo do tego potrzeba pomiarów z kilku okresów.
• MWR zakłada określony średni poziom zainwestowanego kapitału i jej znak (- lub +) będzie zgodny z tym, czy osiągnęliśmy zysk, czy stratę z portfela. Na tej podstawie jest zatem bardziej intuicyjna, ale próba wytłumaczenia jej interpretacji jest karkołomna. Stopa ta po prostu nie ma dobrej interpretacji.
• MWR nie jest uznawana przez żadne standardy rynkowe dla branży finansowej, w tym najważniejsze standardy GIPS.
  

Ze względu szczególnie na wytłuszczone charakterystyki MWR nie używamy jej w Squaberze, choć jest to formalnie stopa adekwatna dla inwestora indywidualnego z powodu jego kontroli nad wpłatami i wypłatami z portfela.

Stopa TWR (Time-Weighted Return), czyli ważona czasem

TWR jest stopą o wiele prostszą w zrozumieniu i opierającą się na realistyczniejszych założeniach, aniżeli MWR. Stopa ważona czasem nie uwzględnia wpływu zewnętrznych przepływów, a więc wpłat i wypłat rzutujących na wielkość zainwestowanego kapitału. Rozwiązuje się zatem postawiony na wstępie problem, gdzie nagle prosta stopa zwrotu wykazywała 200%. Zakładamy, że jako zarządzający nie mamy kontroli nad zewnętrznymi przepływami i to jest założenie adekwatne dla zarządzających w funduszach inwestycyjnych. Nie jest to zatem naginanie rzeczywistości. Inwestor indywidualny co prawda ma kontrolę nad wpłatami i wypłatami, jednak TWR ma kilka zalet względem MWR, które przeważają na jej korzyść.

By wyliczyć TWR dzielimy po prostu okres pomiaru na sub-okresy, każdy w którym nie występuje przepływ zewnętrzny. Ich liczbę determinuje rozłożenie tych przepływów w czasie, możemy np. przyjąć okresy dzienne, co eliminuje większość problemów (nie wchodzimy na poziom zmian kapitału w ciągu dnia, to już etap zaawansowany). W każdym takim dniu czy okresie mierzymy prostą stopę zwrotu. Bierzemy po prostu:

(wartość końcowa dnia – wartość początkowa dnia) / wartość początkowa dnia

Potem mając takie stopy dzienne, czy sub-okresowe, wystarczy je przez siebie przemnożyć dzień po dniu (1+TWR z poniedziałku) * (1+TWR z wtorku) * (1+TWR z środy), itd. Potem odejmujemy od końcowego wyniku 1 i voila. Mamy nasze skumulowane TWR za cały okres, możemy przy tym oglądać jego zmiany dzień po dniu. Za każdym razem, gdy zmienia nam się poziom zainwestowanego kapitału, po prostu zmienia się podstawa wartości początkowej dnia, dlatego stopa ta nie rodzi żadnych problemów z wyliczeniem. Jeśli w ciągu dnia mamy jakieś wpłaty/wypłaty, to możemy po prostu założyć, że wystąpiły na koniec dnia.

Skumulowane TWR możemy przybliżyć przemnażając przez siebie stopy MWR za poszczególne okresy. Przy małej liczbie i kwocie zewnętrznych przepływów, błąd przybliżenia będzie raczej mały, ale będzie on potem znacznie wzrastać. Kumulując zatem sub-okresowe MWR nie otrzymujemy skumulowanej MWR, tylko przybliżenie skumulowanej TWR. Warto dodać, że jeśli nie mamy w portfelu żadnych zewnętrznych przepływów, tj. żadnych dodatkowych wpłat i wypłat, to TWR będzie równa po prostu zwykłej, prostej stopie zwrotu.

Podsumowując TWR:

• Stopa ta nie jest zależna od efektu timingu, a zatem od zmian w zainwestowanym kapitale z powodu wpłat i wypłat. Nie zakłada zatem żadnego określonego poziomu kapitału. Jest zatem szczególnie adekwatna dla zarządzających portfelami.
• Ze względu na powyższe jest standardem rynkowym i jako jedyna jest uznawana przez standardy GIPS.
• TWR pozwala na porównania z innymi.
• Nie jest oparta na żadnych nierealistycznych założeniach o stopie reinwestycji.
• Pozwala na analizę zmienności, czyli liczenie odchylenia standardowego wyników, ale tylko jeśli okresy pomiaru są jednakiej długości (np. dzienne, jak w Squaberze).
• Pozwala na analizę dzień po dniu i dekompozycję wyniku.
• Może jednak nie być zgodna z uzyskaniem zysku lub straty. Może wykazywać wynik ujemny przy zysku na portfelu i dodatnią stopę zwrotu przy stracie. Bywa zatem nieintuicyjna, ale prostsze założenia pozwalają na jej logiczną interpretację.

Ważąc zatem wszystkie koszty i korzyści, zdecydowaliśmy się na stopę TWR, mimo, że użytkownicy czasem mają problem z jej zrozumieniem (z powodu rozbieżności znaków). Wierzymy jednak, że ten artykuł wyczerpująco opisał ten temat z perspektywy inwestora indywidualnego i pozwolił na zrozumienie różnych stóp zwrotu. Odpowiadając jednoznacznie na częste pytania: tak, uważamy, że tylko TWR jest adekwatną stopą zwrotu z Twojego portfela, a wynik jest dokładnie taki, jak wskazuje algorytm.