Beta – czym jest i jak się nią posługiwać?

Wstęp

W ramach analizy fundamentalnej opracowano gros metod określania ryzyka. Samo pojęcie ryzyka jest niejednoznaczne i można wyróżnić dwa jego podejścia interpretacyjne: negatywne i neutralne. Negatywne podejście do ryzyka oznacza ewentualność, że oczekiwany wynik z transakcji rozminie się z oczekiwaniami inwestora in minus, to znaczy będzie niższy, niż zakładano lub nawet obróci się w stratę. Ryzyko w ujęciu neutralnym, to zarówno zagrożenie, jak i szansa. Przyjmuje się tutaj również możliwość, że uzyskana stopa zwrotu będzie wyższa, niż zakładano. Ryzyko można starać się ewaluować na różne sposoby. Szeroko wykorzystywanym sposobem jest wykorzystanie ku temu celowi współczynnika Beta (ang. Beta lub risk factor). 

Z lektury tego artykułu dowiesz się:

• czym jest współczynnik Beta i jak jest obliczany,
• jakie wykorzystanie ma w ujęciu teoretycznym,
• jakimi właściwościami się cechuje,
• jak może być praktycznie wykorzystany na giełdzie.

Współczynnik Beta jako miara ryzyka

Beta wskazuje, o ile punktów procentowych zmieni się stopa zwrotu z waloru, jeśli stopa zwrotu wybranego indeksu rynku ulegnie zmianie o 1 procent (Gołębiowski, Tłaczała 2009, s. 212). W swojej istocie zatem wskaźnik ten wyraża stopień korelacji zmian stóp zwrotu z waloru ze zmianami stóp zwrotu z indeksu giełdowego.

Przyjmowanym punktem odniesienia (indeksem) może być wybrany, zawężony zbiór akcji spółek lub indeks szerokiego rynku – obejmujący reprezentatywną jego część lub wszystkie notowane spółki. Dla akcji spółek z polskiej Giełdy Papierów Wartościowych, Betę wylicza się w odniesieniu do indeksu WIG, obejmującego spółki z rynku podstawowego, które spełniają kryteria procentu i wartości akcji w wolnym obrocie. WIG jest najszerszym indeksem rynku w Polsce, stąd stanowi on naturalny wybór do obliczeń – tak też jest w Squaberze.

Beta może zostać wyliczona na kilka sposobów. Często przywołuje się nieco bardziej skomplikowany w obliczeniach sposób wykorzystujący kowariancję i wariancję stóp zwrotu. W takim ujęciu Betę wyraża się jako:

Beta = Cov(w,i)/Var(i) 

Gdzie:

Con(w,i) – kowariancja stóp zwrotu wybranego waloru i indeksu,

Var(i) – wariancja stóp zwrotu wybranego indeksu.

Istnieje również sposób prostszy, wynikający z pierwotnego znaczenia współczynnika. Wywodzi się on z prostej koncepcji regresji liniowej typu y = a + bx, będącej niczym innym, jak postacią kierunkową funkcji liniowej. Współczynnik b (Beta) odpowiada w niej za nachylenie funkcji względem osi x (będąc współczynnikiem kierunkowym). Adaptując regresję dla naszych celów można stworzyć funkcję wyznaczającą zależność zmian stopy zwrotu waloru od zmian stopy zwrotu rynku:

Sw = a+ b * Si + ε

Gdzie:

Sw – stopa zwrotu z waloru,

Si – stopa zwrotu z indeksu,

ε – zmienna losowa.

Dla tak przedstawionego równania, Betę wyznacza się prostym wzorem znanym z liceum. Można w tym celu użyć również funkcji =NACHYLENIE w Excelu, gdzie za zbiór y przyjmujemy stopy zwrotu waloru, a x – indeksu. Nie ma przy tym znaczenia, którym z omówionych sposobów obliczymy Betę, oba powinny prowadzić do tych samych jej wartości. Wartości współczynnika mogą ulegać zmianie po każdej sesji, stąd duże znaczenie będzie miała przyjęta długość okresu obliczeń, co zostanie omówione w dalszej części artykułu. 

Beta w ujęciu teoretycznym

Wskaźnik Beta stanowi niejako trzon najpopularniejszych modeli rynku kapitałowego, służących chociażby wycenie akcji. Wzór funkcji liniowej, który podaliśmy powyżej, jest w istocie rzeczy równaniem modelu jednowskaźnikowego Sharpe’a. Beta w tym modelu jest miarą wrażliwości, a do jej obliczeń można wykorzystywać nie tylko historyczne dane o stopach zwrotu, lecz także wszelkie inne informacje o analizowanej spółce. Obliczone w ten sposób dwie Bety są następnie uśrednione średnią ważoną. 

Obliczony wskaźnik może być również interpretowany jako miara ryzyka systematycznego akcji, a więc ryzyka rynku niepodlegającego dywersyfikacji (nie można go wyeliminować, choć teoretycznie da się stworzyć portfel z Betą zerową). Ryzyko to jest tym wyższe, im wyższy (lub niższy dla wartości ujemnych) jest współczynnik Beta. Podobnie sprawa ma się w nieco bardziej zaawansowanych modelach CAPM i APM(APT). 

Betę można wyliczyć również dla portfela akcji, gdzie Beta portfela jest po prostu sumą poszczególnych Bet akcji spółek, wchodzących w skład portfela, którym przypisuje się wagi zgodnie z ich udziałem w portfelu. Należy zauważyć, że Beta instrumentu wolnego od ryzyka wynosi 0 (Jajuga, Jajuga 2008, s. 237-254).

Właściwości Bety

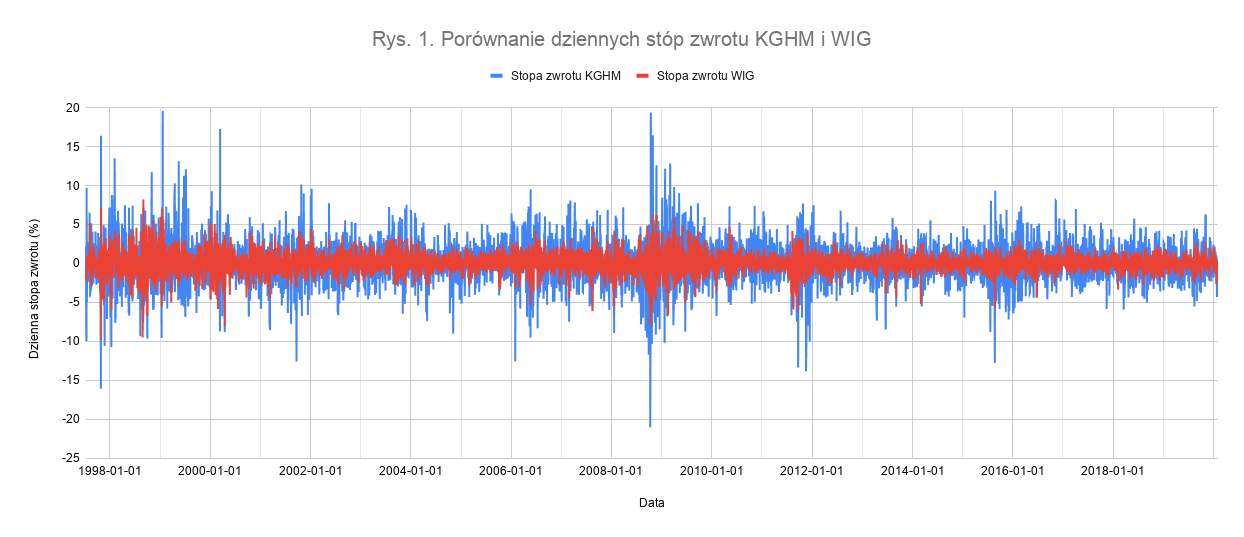
Beta jest miarą średnią i jedynie przybliża potencjalne zmiany stóp zwrotów z walorów. Jako, że centralnymi zmiennymi dla Bety są stopy zwrotów waloru i indeksu, sprawdźmy jak przykładowo mogą się one kształtować. Zostało to przedstawione na rysunku 1, gdzie porównano dzienne stopy KGHM i WIG.

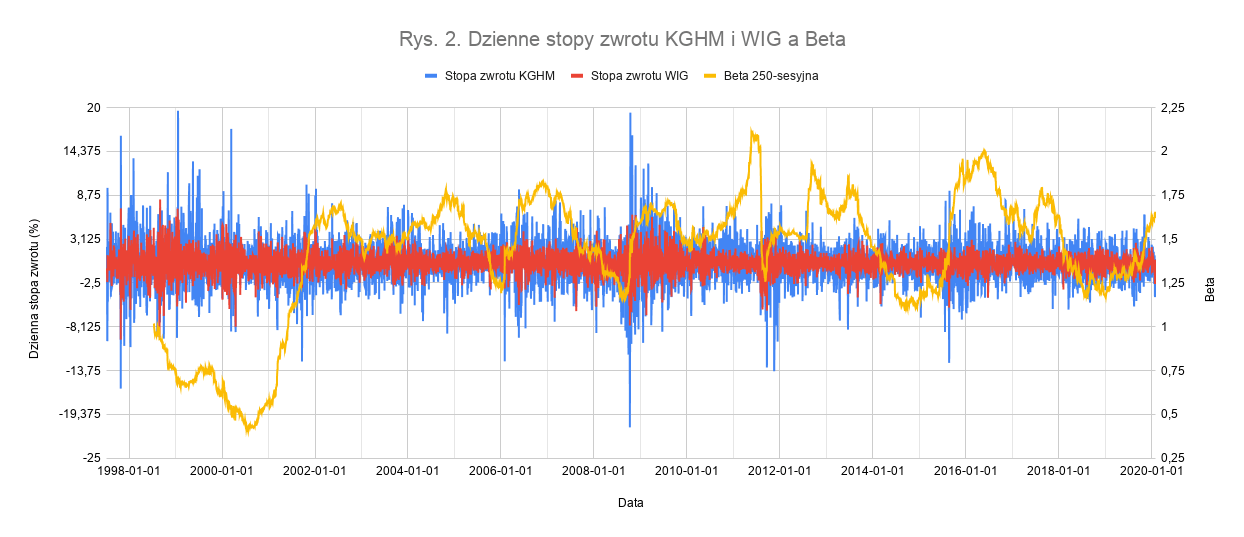
Dzienna stopa zwrotu to oczywiście miara względna (podawana w %), wyrażana wzorem: (Ct – Ct-1)/Ct-1, gdzie Ct to dzisiejsza cena zamknięcia, a Ct-1 – wczorajsza. Jak możemy zaobserwować na wykresie, dzienne stopy zwrotu WIG były niejako obejmowane przez stopy KGHM przez niemalże cały okres notowań na GPW tego drugiego. Wyższe słupki niebieskie dla KGHMu oznaczają, że reagował on silniej, niż wybrany indeks szerokiego rynku, a zatem można zakładać, że Beta będzie wyższa od jedności (wzrost WIG o 1% oznaczał średnio wyższy wzrost dla KGHM i analogicznie dla spadków). Czy tak jednak było zawsze? Sprawdźmy jak 250-sesyjna Beta KGHMu kształtowała się na przestrzeni lat. Na rysunku 2. został na żółto nałożony jej przebieg (wartości Bety wyrażane są na skali po stronie prawej).

Warto zauważyć pewną oczywistą właściwość. Beta 250-sesyjna możliwa jest do obliczenia dopiero po upływie 251 sesji od początku notowań danego waloru. 1 dodatkowa sesja wiąże się z faktem, że dopiero po zakończeniu drugiego dnia notowań waloru można wyznaczyć pierwszą, dzienną stopę jego zwrotu. Jak możemy zaobserwować, wartości Bety na przestrzeni dwóch dekad ulegały fluktuacją. Co więcej, do 2002 roku kształtowała się ona na poziomach niższych od jedności, jednak nigdy nie znalazła się poniżej zera. Począwszy od 2002 roku, Beta dla KGHMu dosyć regularnie konsolidowała w przedziale około 1,15 – 2. 

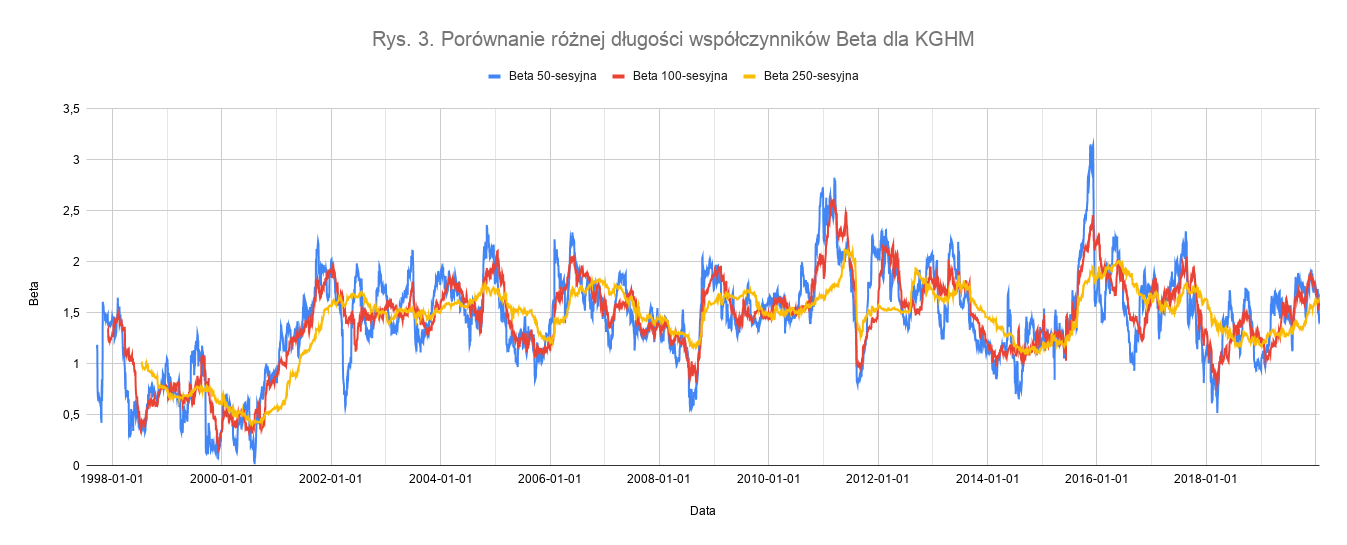
Im dłuższy okres Bety, tym bardziej wygładzony jej wykres (jak w średnich kroczących). Przyjmowane 250 sesji wydaje się dość rozsądną wartością, zapewniającą względną stabilność odczytów, jednak nie pozbawiających ich określonej dynamiki zmian. Jak jednak wyglądają Bety krótsze? Wskaźniki o długości 50, 100 i 250 sesji zostały porównane na rysunku 3.

Wszystkie trzy Bety zachowują ten sam kierunek zmian, jednak im krótszy wskaźnik, tym silniejsze są jego oscylacje i nagłe skoki wartości (można to przyrównać do tzw. szumu niskich interwałów czasowych dla wykresów cen). Co więcej, krótsze Bety są w tym wypadku na ogół wyższe/niższe, niż Beta najdłuższa, która je uśrednia.

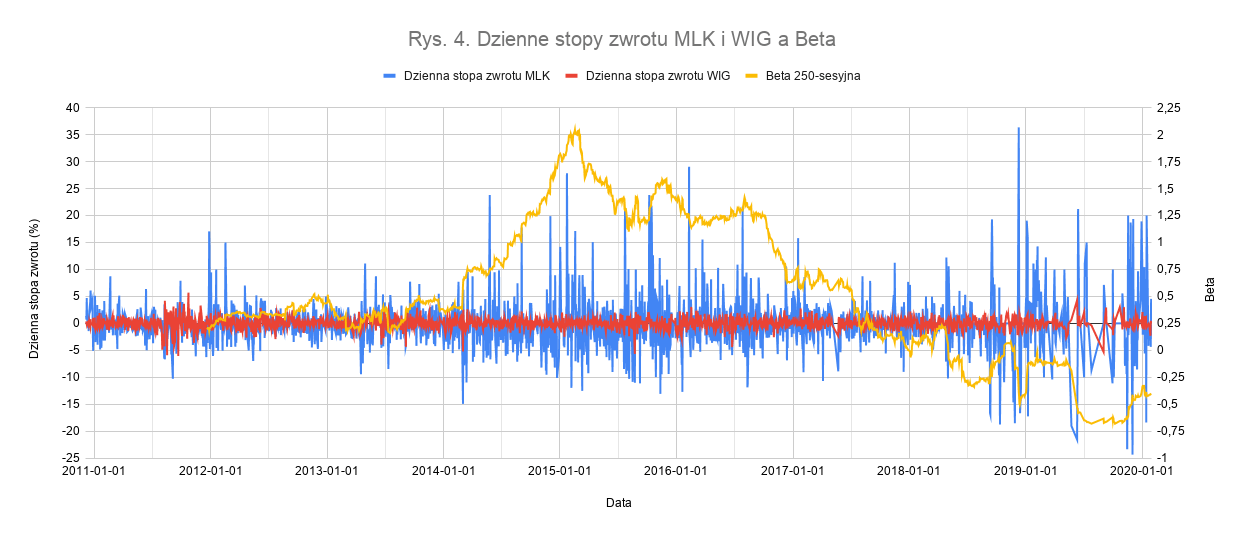
Spójrzmy jeszcze jak wygląda Beta ujemna. Na moment pisania tego artykułu, najwięcej walorów z Betą ujemną występuje na rynku NewConnect, dla nich też ten wskaźnik osiąga najniższe wartości. Na ten moment jednymi z najniższych wartości Beta na rynku głównym GPW cechuje Milkiland N.V. – MLK. Po wyeliminowaniu dni, kiedy walor ten nie miał notowań, wykres 250-sesyjnej Bety na tle stóp zwrotu przedstawia się tak, jak na rysunku 4. 

Beta dla waloru zeszła do wartości ujemnych na początku 2018 roku i jak na razie taką pozostaje. Warto zauważyć jednak, że wcześniej bywała ona bardzo wysoka, osiągając nawet poziom 2. Małe zagęszczenie stóp zwrotu w ostatnich miesiącach jest spowodowane przerwami w notowaniach akcji tej spółki.

Beta w praktyce giełdowej

Wartości osiągane przez wskaźnik Beta można w praktyce podzielić na trzy przedziały. Akcje o Becie większej od 1 można uznać za agresywne: cechują się większym ryzykiem, podlegając silniejszym zmianom, ale również potencjalnie wyższą zyskownością (zgodnie z neutralną koncepcją ryzyka). Przykładowo przy Becie równej 1,5 zmiana wartości WIG o 1 procent przekłada się na przeciętne zmiany stopy zwrotu waloru o 1,5 pkt. proc. Walory cechujące się Betą z przedziału od 0 do 1 mają niższe ryzyko, niż rynek, co okupione jest niższą zyskownością – są defensywne. Przy Becie równej 0,5, zmiana WIG o 1 procent przełoży się na średnią zmianę stopy zwrotu z waloru o 0,5 pkt. proc. Trzecią grupą akcji są te, mające Betę ujemną – mniejszą od zera. Występują relatywnie rzadko i poruszają się wbrew rynkowi. Przykładowo dla Bety równej -1,5, wzrost WIGu o 1 procent da spadek stopy zwrotu z waloru średnio o 1,5 pkt. proc. W dziedzinie wartości ujemnych im niższa Beta, tym wyższe ryzyko i (odwrotna) zyskowność. Akcje o Becie równej 1 są rzecz jasna zgodne ze średnią rynkową, poruszając się na ogół w analogiczny sposób i będąc przeciętnie równie zyskownymi, zaś te, o Becie zerowej, nie ulegają zmianie, w momencie zmiany indeksu rynkowego.

Co do zasady, ogół akcji notowanych na rynku cechuje się Betą zbliżoną do 1 i zachowuje się podobnie, jak cały rynek. Betę w okolicach 0 mogą mieć firmy, których działalność koncentruje się na branżach bezpiecznych, tj. w znacznej mierze niezależnych od rynku, chociażby wydobywanie złota czy energetyka. Zdarza się to jednak raczej na giełdach amerykańskich, niż polskim GPW. W tworzeniu portfeli inwestycyjnych unika się akcji o wysokiej Becie (>1), jako że zwiększają one ogólne ryzyko portfolio, choć niektórzy inwestorzy mogą dążyć do wzmożonej ekspozycji na ryzyko. Osoby posiadające awersję do ryzyka z kolei poszukują do swych portfeli walorów o Becie niskiej (<1) lub nawet ujemnej, których włączenie zmniejsza co prawda zyskowność portfolio, jednak przy tym znacznie redukuje jego ryzyko. Należy pamiętać, że działa to jedynie w połączeniu z innymi akcjami o Becie dodatniej, jako że walory o ujemnej Beta same w sobie mogą być ryzykowne. Teoretycznie rzecz biorąc, na rynku w stanie równowagi akcje z wysoką Betą powinny być tanie i oferować perspektywy wysokich zysków, co rekompensuje ich ryzyko. Akcje o niskiej Becie zaś powinny cieszyć się relatywnie wysokim popytem ze strony inwestorów i być z tego względu drogie, cechując się niskimi stopami zwrotu (Begg et al. 2014, s. 477-480)

Podsumowanie

Współczynnik Beta można uznać za miarę ryzyka akcji. Mierzy on zmianę stopy zwrotu z akcji przy zmianie wartości indeksu o 1 procent. Z tego względu Bety powyżej 1 znaczą akcje agresywne (silniej reagujące, niż indeks), zaś te między 0 a 1 – defensywne (słabiej reagujące). Beta 1 oznacza zmiany zgodne z indeksem, zaś 0 – brak powiązania. Wartości ujemne Bety to odwrotna zależność, przy czym również tutaj można wyróżnić akcje ujemnie defensywne i ujemnie agresywne. 

Beta może być liczona na różne sposoby, które jednak prowadzą do tych samych wyników. Jest to wskaźnik dynamiczny, którego wartości podlegają zmianie po każdej sesji. Należy pamiętać jednak, że istotną zmienną jest przyjmowana długość okresu dla obliczeń. Im on dłuższy, tym bardziej wygładzony przebieg wskaźnika i mniejsze jego wahania. Krótkie Bety charakteryzują się silniejszymi zmianami na przestrzeni czasu. 

Literatura

Begg D., Vernasca G., Fischer S., Dornbusch R. (2014), Mikroekonomia, Polskie Wydawnictwo Ekonomiczne, Warszawa.
Gołębiowski G., Tłaczała A. (2009), Analiza finansowa w teorii i praktyce, Difin, Warszawa.
Jajuga K., Jajuga T. (2008), Inwestycje: instrumenty finansowe, aktywa niefinansowe, ryzyko finansowe, inżynieria finansowa, Wydawnictwo Naukowe PWN, Warszawa.